Many new traders start off by trying to maximize their percentage of winning trades, the obvious thinking being that the more I win, the better my trading results will be. Although this is not incorrect, it is certainly not the full story. What many would-be traders don’t know is that it is quite possible to have a win percentage well above 50% and still lose money, and that there are some professionals out there who might only have a winning percentage as low as 30% yet still make money.
What traders need to be trying to maximize is their expectancy. Expectancy is a statistical concept that speaks to an expected payoff over numerous trials. The equation is:
E = (W x R) – [(1-W) X L]
Where
E = Expectancy
W= Probability of winning (win percentage)
R = Reward of a winning trade
L = Loss of a losing trade
Maximizing expectancy
For those who are not mathematically inclined do not fear, it is the conclusion that is important, more than the underlying maths.
There are two parts to the expectancy equation
- Probability of winning or your win percentage – this is the part of the equation that most new comers focus on.
- Risk/Reward ratio – this is the often neglected part of the equation when trying to become a profitable trader
Risk/Reward ratio is the average size of a winning trade divided by the average size of a losing trade. The graph below illustrates an individual trade where the Risk/Reward ratio is 3.21.
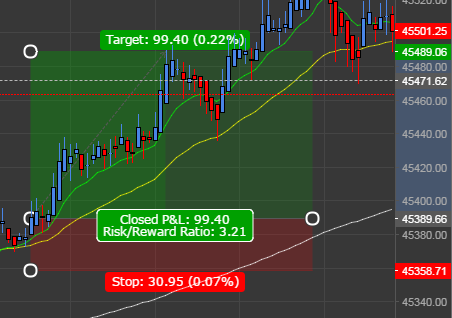
Obviously the higher this number the better. By maintaining a consistently large Risk/Reward ratio it is possible to have a probability of winning well below 50% and have a positive expectancy (i.e. make money in the long run).
By doing some basic arithmetic to the expectancy equation we can come to some interesting conclusions. Assuming that the long term expectancy = 0 (i.e. our trader will break even)
W X R = (1-W) x L
R / L = (1-W) / W
It is now possible to plot the risk reward relationship on a chart and the various break even points.
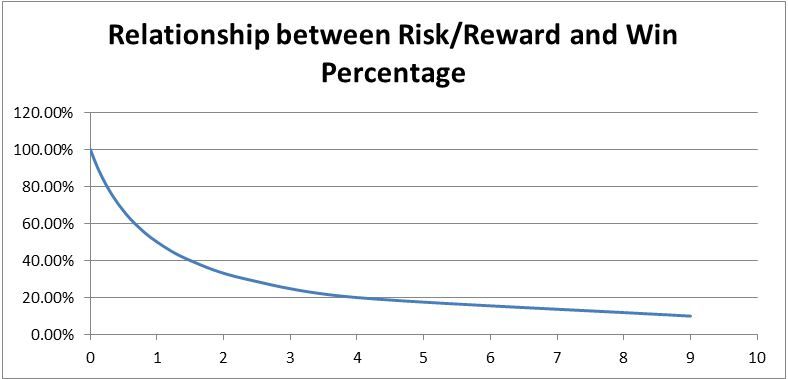 X=Risk/Reward Ratio, Y=Percentage of winners
X=Risk/Reward Ratio, Y=Percentage of winners
A trader should use this chart in the following way.
If you have a win percentage of 50%, in order for you to break even your average winner must be equal to your average loser (Risk/Reward =1). If you have calculated that your win percentage is 50% then you should always aim ensure that you will make more money if your trade is a winner than you you would lose if it were a loser. Otherwise at best you will break even.
If you have a win percentage of 30% then to break even you would need your average winner to be 2.3 times the size of your average loser. (Risk/Reward = 2.3) Therefore, if your anticipated win percentage is 30% do not take any trade unless your potential risk/reward is larger than this.
When starting out a trader should primarily be thinking about maximizing expectancy, and when deciding on your trading method consider always keeping the risk/reward ratio on your side, not just the percentage win rate.

